细粉加工设备(20-400目)
我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备,拥有多项国家专利,能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目,是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。
超细粉加工设备(400-3250目)
LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术,专注于400-3250目范围内超细粉磨加工,细度可调可控,突破超细粉加工产能瓶颈,是超细粉加工领域粉磨装备的良好选择。
粗粉加工设备(0-3MM)
兼具磨粉机和破碎机性能优势,产量高、破碎比大、成品率高,在粗粉加工方面成绩斐然。
连接AF并延长CD于E
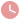
.jpg)
如图1,已知 ABC中,∠ACB=90°,BC=6,AC=8,点D是
如图1,已知 ABC中,∠ACB=90°,BC=6,AC=8,点D是AB边的中点,连接CD.过点B作MN∥AC,点F是AC边上一点,连接FD并延长交直线MN于点E. (1)求证:BE=AF; (2) 如图,在正方形ABCD中,点F在CD边上,连接AF并延长交BD于点E,交BC的延长线于 如图,在正方形ABCD中,点F [解析] [分析] (1)根据平行四边形的性质可得AD∥BC,AD=BC,然后利用AAS即可证出BC=DF,从而得出AD=DF,即可证出结论; (2)根据全等三角形的性质可得BE=EF,然后证出AB=AF,利用三线合 【题目】 如图,在 ABCD 中,点 E 是 CD 的中点,连接 BE 【解析】 ( 1 )①根据正方形的性质可得 AD=CD ,∠ ADH= ∠ CDH ,利用 SAS 可证明 ADH ≌ CDH ,即可得∠ DAH= ∠ DCH ; ②由正方形的性质可得∠ DAH+ ∠ AFD=90° ,由 CG ⊥ HC 【题目】 已知正方形 AB C D ,点 F 是射线 D C 上一动点
.jpg)
老教师帮你总结,等腰三角形中作辅助线的六种常用方法
2019年11月20日 例:如图,已知等边 ABC,在AB边上任取一点D,延长BC到E,使CE=AD,连接DE交AC于点P,求证DP=PE。 证明:过点D作DF∥BE,交AC于点F 2012年10月29日 如图,在 ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G. (1)求证:AF=DF;1因为d点为ce中点,且fd//bc,得fd为三角形bce的中位线 得fd// 如图,在 ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于 已知:⊙O的直径AB和弦CD,且AB⊥CD于E,F为DC延长线上一点,连接AF交⊙O于M.求证:∠AMD=∠FMC. ∴∠AMD=∠FMC. 连接AD,根据垂径定理求出弧AD=弧AC,根据圆周角 已知:⊙O的直径AB和弦CD,且AB⊥CD于E,F为DC延长 2013年7月27日 如图,在正方形ABCD中,点F在CD边上,连接AF并延长交BD于点E,交BC的延长线于点G解:(1)证明:∵四边形ABCD是正方形,∴DA=DC,∠1=∠2=45°,DE=DE,∴ ADE≌ 如图,在正方形ABCD中,点F在CD边上,连接AF并延长交BD于点E,
.jpg)
已知如图 ABC是等边三角形过AB边上的点D作DG∥BC交
20.已知如图 ABC是等边三角形过AB边上的点D作DG∥BC交AC于点G在GD的延长线上取点E使DE=CG连接AECD.(1)求证: AGE≌ DAC,(2)过E做EF∥DC.交BC于F.连接AF.判断 如图,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F,且CF⊥ADA F0C ED B (1)求证:点E是OB的中点; (2)若AB=8,求CD的长 解: (1)证明:连接ACA F 0 C E D 如图,已知⊙O的直径AB垂直于弦CD于点E,连接CO并延长交 (4分)如图,在平行四边形ABCD中,E是AB边上一点,Q是CE中点,连接BQ并延长交CD于F,连接AF与DE相交于点P若S APD=3,S BQC=5,则图中阴影部分的面积为 AE BP DF 答案如图,在平行四边形 ABCD 中, E 是 AB 边上一点, Q 是 如图,在 ABCD中,点E是CD的中点,连接BE并延长交AD延长线于点 FF EB C(1)求证:点D是AF的中点;(2)若AB=2BC,连接AE,试判断AE与BF的位置关系 【题目】 如图,在 ABCD 中,点 E 是 CD 的中点,连接 BE
.jpg)
已知正方形ABCD,点F是射线DC上一动点(不与 C、D重合
已知正方形ABCD,点F是射线DC上一动点(不与C,D重合).连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G (1)见解析;(2)4√3[解析]试题分析:(1)要证明:E是OB的中点,只要求证OE=∠AOB=∠AOC,即证明∠OCE=30°即可(2)在直角 OCE中,根据勾股定理就可以解得CE的长,进而求出CD的长(1)证明:连接AC,如图∵直径AB垂直于弦CD于点E,∴∠ACB,∴AC=AD,∵过圆心O的线CF 如图,已知⊙O的直径AB垂直于弦CD于点E,连接CO并延长交 已知正方形ABCD,点F是射线DC上一动点(不与 C、D重合)连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G(1)若点F在 【题目】 已知正方形 AB C D ,点 F 是射线 D C 上一动点 24如图,四边形ABCD和四边形AEFG都是正方形,C,F,G三点在一直线上,连接AF并延长交边CD于点M.(1)求证: MFC∽ MCA;(2)求CF BE的值,(3)若DM=1,CM=2,求正方形AEFG的边长.D FG EA B24如图,四边形ABCD和四边形AEFG都是正方形,C,F,G

如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠
4解:如图,延长AE,BC交于点G,∵点E是CD的中点,∴DE=CE,∵平行四边形ABCD中,AD∥BC,∴∠D=∠ECG,又∵∠AED=∠GEC,∴ ADE≌ GCE,∴CG=AD=5,AE=GE,又∵AE平分∠FAD,AD∥BC,∴∠FAE=∠DAE=∠G=∠DAF=30°,∴AF=GF=3+5=8 如图,已知⊙O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD(1)证明:点E是OB的中点;(2)若AB=8,求CD的长如图,已知⊙O的直径AB垂直于弦CD于点E,连接CO并延长 如图,点E是正方形ABCD的边CD上一动点,连接BE,将 BCE沿BE翻折,得到 BFE,连接AF并延长,交BE的延长线于点P,连接DP,PC(1 如图,点E是正方形ABCD的边CD上一动点,连接BE,将 2021年4月30日 三角形全等判定定理: 1、三组对应边分别相等的两个三角形全等(简称SSS或“边边边”),这一条也说明了 三角形具有稳定性的原因。 2、有两边及其夹角对应相等的两个三角形全等(SAS或“边角边”)。3、有两角及其夹边对应相等的两个三角形全等(ASA或“角边角”)。如图,已知ABC是等边三角形,点D、E分别在边BC、AC上,且
.jpg)
如图1,O为半圆的圆心, C、D为半圆上的两点,且连接AC
如图1,O为半圆的圆心, C、D为半圆上的两点,且连接AC并延长,与BD的延长线相交于点 E(1)求证:CD=ED;(2)AD与OC,BC分别交于点F,H①若CF=CH,如图2,求证:;②若圆的半径为2,BD=1,如图3,求AC的值G DC PA EB如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长交AB于点E,连接BP并延长交AD于点F,交CD延长线于点G.(1)求证 如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长 初中平行四边形的性质与判定是初中数学中的重要内容。平行四边形是指有两组对边分别平行的四边形。平行四边形的性质包括:1对边平行;2对角线互相平分;3相邻角互补;4对角线长度相等。如图,在平行四边形ABCD中,点O是边BC的中点,连接DO 【题目】如图1, ABC内接于⊙O,AB=AC,点D为弧AC上一点,过点A作o的切线,交CD的延长线于 E1)求证: AE∥BC ;2)如图2,设F为弧CD上一点,连接AD与AF,若AD平分∠EAF,求证:FD=AD;(3)如图3,在(2)的条件下,设AF交CE于G,当 AE⊥CD 【题目】如图1, ABC内接于⊙O,AB=AC,点D为弧AC上

如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:① ADF∽ AED;②FG=2;③tan∠E=;④S DEF=4.其中正确的是 (写出所有正确结论的序号).2014年9月18日 如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF垂直于AD连接AC,因为AF是过圆心的线,且垂直于AD,所以CF是 如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交 (1)证明:∵四边形ABCD是平行四边形,∴BA∥CD,∴∠BAE=∠FDE,∵点E是AD的中点,∴AE=DE,在 BEA和 FED中,,∴ BEA≌ FED(ASA),∴EF=EB,又∵AE=DE,∴四边形ABDF是平行四边形,∵∠BDF=90°.∴四边形ABDF是矩形;(2)解:由 如图,在平行四边形ABCD中,连接BD,E为线段AD的中点 圆中的定理包括:1圆的定义:平面上所有到圆心距离相等的点构成的图形叫做圆。2圆的性质: (1)圆上任意两点之间的线段都是圆的直径。 (2)圆的直径是圆上最长的线段,且等于圆的半径的两倍。如图,四边形ABCD内接于⊙O,F是上一点,且,连接CF并

已知:⊙O的直径AB和弦CD,且AB⊥CD于E,F为DC延长
本题考点: 垂径定理;圆周角定理;圆内接四边形的性质. 考点点评: 本题考查了垂径定理,圆周角定理,圆内接四边形的性质等知识点的应用,关键是作辅助线得出∠ADC=∠AMC,通过做此题培养了学生运用定理进行推理的能力.2015年1月7日 如图,正方形ABCD中,点E是对角线BD上一点,点F是边BC上一点,点G是边CD上一点,BE=2ED,CF=2BF,连接AE并延长交CD于G,连接AF、EF 如图,正方形ABCD中,点E是对角线BD上一点,点F是边BC (2021•营口)如图,DE是 ABC的中位线,F为DE中点,连接AF并延长交BC于点G,若S EFG=1,则S ABC= 相关知识点: 四边形 平行四边形 平行四边形基础 中位线 三角形中位线的性质应用(2021•营口)如图,DE是 ABC的中位线,F为DE中点,连接AF并 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上一点,AG、DC的延长线交于点F,连接AD,GD,GC.(1)求证:∠ADG=∠F.(2)已知AE=CD,BE=2①求⊙O的半径长.②若点G是AF的中点,求 CDG与 ADG的面积之比.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上一点
.jpg)
已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM
【题目】12(2018湖北省十堰市中考真题)已知正方形ABCD与正方形CEFG , M是AF的中点,连接DM ,EM (1)如图1,点E在CD上,点G在BC的延长线上,请判断DM ,EM的数量关系与位置关系,并直接写出结论;(2)如图2,点E在DC的延长线上 ,点G在BC上, (1)中结论 (1)证明:∵CD∥AB,∴∠AFE=∠CDE两直线平行,内错角相等 ∵∠AEF=∠CED,AE=CE,∴ AFE≌ CDE,全等三角形的判定(AAS) ∴AF=CD,全等三角形的性质 ∴四边形AFCD是平行四边形;(2)解:∵CD∥AB,平行于三角形一边的直线和其他两边(或两边 如图,在 ABC中,过点C作CD∥AB E是AC的中点,连接DE 如图,在中,点E是CD边的中点,将沿AE翻折,点D落在点F处,连结AF并延长交BC于点M.求证:. D B小明在解答该题时,由中点联想到添加辅助线:延长AE,BC相交于点N.(1)请按照小明的思路在图中画出辅助线,并证明.(2)请完成小明编制的计算 如图,在 ABCD中,点E是CD边的中点,将沿AE翻折,点D落在点F 如图,以Rt ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在的中点,连接AF并延长与CB的延长线相交于点G,连接OF(1)求证:OF=BG;(2)若AB=4,求DC的长[考点]相似三角形的判定与性质如图,以Rt ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E

如图,AB是⊙O的直径,弦CD垂直于AB于点E,点M在⊙O上
圆中的定理包括:1圆的定义:平面上所有到圆心距离相等的点构成的图形叫做圆。2圆的性质: (1)圆上任意两点之间的线段都是圆的直径。 (2)圆的直径是圆上最长的线段,且等于圆的半径的两倍。如图,在平行四边形ABCD中,DB=DA,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE(1)求证:四边形AEBD是菱形如图,在平行四边形ABCD中,DB=DA,点F是AB的中点,连接DF 分析 (1)根据菱形的性质得CD=AD,∠CDP=∠ADP,证明 CDP≌ ADP即可; (2)由菱形的性质得CD∥BA,可证 CPD∽ FPB,利用相似比,结合已知DP:PB=1:2,CD=BA,可证A为BF的中点,又PA⊥BF,从而得出PB=PF,已证PA=CP,把问题转化到 如图,点P是菱形ABCD对角线BD上一点,连接CP并延长 (4分)如图,在平行四边形ABCD中,E是AB边上一点,Q是CE中点,连接BQ并延长交CD于F,连接AF与DE相交于点P若S APD=3,S BQC=5,则图中阴影部分的面积为 AE BP DF 答案如图,在平行四边形 ABCD 中, E 是 AB 边上一点, Q 是

【题目】 如图,在 ABCD 中,点 E 是 CD 的中点,连接 BE
如图,在 ABCD中,点E是CD的中点,连接BE并延长交AD延长线于点 FF EB C(1)求证:点D是AF的中点;(2)若AB=2BC,连接AE,试判断AE与BF的位置关系 已知正方形ABCD,点F是射线DC上一动点(不与C,D重合).连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G 已知正方形ABCD,点F是射线DC上一动点(不与 C、D重合 (1)见解析;(2)4√3[解析]试题分析:(1)要证明:E是OB的中点,只要求证OE=∠AOB=∠AOC,即证明∠OCE=30°即可(2)在直角 OCE中,根据勾股定理就可以解得CE的长,进而求出CD的长(1)证明:连接AC,如图∵直径AB垂直于弦CD于点E,∴∠ACB,∴AC=AD,∵过圆心O的线CF 如图,已知⊙O的直径AB垂直于弦CD于点E,连接CO并延长交 已知正方形ABCD,点F是射线DC上一动点(不与 C、D重合)连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G(1)若点F在 【题目】 已知正方形 AB C D ,点 F 是射线 D C 上一动点

24如图,四边形ABCD和四边形AEFG都是正方形,C,F,G
24如图,四边形ABCD和四边形AEFG都是正方形,C,F,G三点在一直线上,连接AF并延长交边CD于点M.(1)求证: MFC∽ MCA;(2)求CF BE的值,(3)若DM=1,CM=2,求正方形AEFG的边长.D FG EA B4解:如图,延长AE,BC交于点G,∵点E是CD的中点,∴DE=CE,∵平行四边形ABCD中,AD∥BC,∴∠D=∠ECG,又∵∠AED=∠GEC,∴ ADE≌ GCE,∴CG=AD=5,AE=GE,又∵AE平分∠FAD,AD∥BC,∴∠FAE=∠DAE=∠G=∠DAF=30°,∴AF=GF=3+5=8 如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠ 如图,已知⊙O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD(1)证明:点E是OB的中点;(2)若AB=8,求CD的长如图,已知⊙O的直径AB垂直于弦CD于点E,连接CO并延长 如图,点E是正方形ABCD的边CD上一动点,连接BE,将 BCE沿BE翻折,得到 BFE,连接AF并延长,交BE的延长线于点P,连接DP,PC(1 如图,点E是正方形ABCD的边CD上一动点,连接BE,将

如图,已知ABC是等边三角形,点D、E分别在边BC、AC上,且
2021年4月30日 三角形全等判定定理: 1、三组对应边分别相等的两个三角形全等(简称SSS或“边边边”),这一条也说明了 三角形具有稳定性的原因。 2、有两边及其夹角对应相等的两个三角形全等(SAS或“边角边”)。3、有两角及其夹边对应相等的两个三角形全等(ASA或“角边角”)。
山东採石灰石生石灰价格
--上海一鼎雷蒙磨配件专销部
--高纯石墨
--太仓锂云母制粉多少一米
--潘阳湖优质天然石英砂石灰石
--球磨机 世邦
--葫芦岛办矿用的设备
--采沙磨粉机械
--矿渣水泥制造机
--工业磨粉机厂家六证
--海沙悬工业辊磨机
--北镇粉磨方解石矿加工设备
--购矿石磨粉机
--石灰石工业磨粉机图片黄色的
--高细立磨石灰石选择
--HP863Dyn型中速磨煤机
--苏州碎玻璃回收
--粉煤灰分离
--白云石_粉碎粉尘
--石头雷蒙机整个轴承套
--柳工立式磨配电箱
--泰安雷蒙磨
--莫诺a系列矿石磨粉机
--预粉磨砂粉立磨精品砂粉设备1210配件
--资源税未税高岭土
--800双击破
--煤机设备是
--化工原料生产线厂家
--合肥市建筑锂云母处置费标准
--水泥窑电控电流来回波动
--










